Tiesinė Funkcija: Apibrėžimas ir Savybės

Tiesinė funkcija, dažnai žinoma kaip afinitoji funkcija, yra matematinė funkcija, kuri gali būti išreikšta formulėmis f(x) = kx + b. Čia k ir b yra realieji skaičiai, o k ≠ 0. Tiesinės funkcijos yra svarbios matematikos ir kitų mokslų srityse, nes jos padeda apibūdinti tiesinę priklausomybę tarp dviejų kintamųjų.

Grafikas ir Kampinis Koeficientas

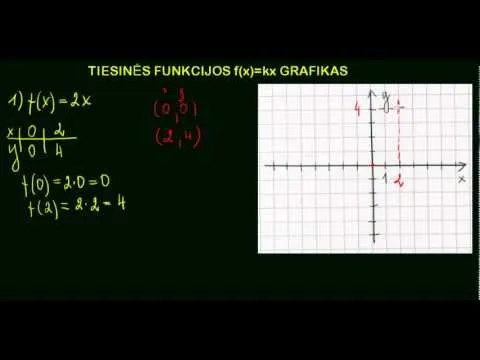
Tiesinės funkcijos grafikas yra tiesė, kuri eina per tašką (0, b) ir formuoja kampą φ su teigiamąja abscisių ašimi. Kampo tangentas, tg φ, yra lygi k, kuris vadinamas kampiniu koeficientu. Jei b = 0, tai funkcija vadinama homogenine.

Tiesinių Funkcijų Savybės

• Reikšmių pokytis yra tiesiogiai proporcingas argumentų pokyčiui.
• Grafikas visada yra tiesė linija.
• Tiesinės funkcijos gali būti homogeninės, kai b = 0.
• Fizikoje ir technikoje tiesinės funkcijos dažniausiai naudojamos aprašyti įvairių dydžių tiesinę priklausomybę.
• Jei funkcijos argumentas ir pati funkcija yra tiesinių erdvių elementai, tada homogeninė funkcija tampa tiesiniu operatoriumi.

Tiesinės Funkcijos Taikymas

Tiesinės funkcijos yra plačiai naudojamos tiek teorinėje, tiek praktinėje veikloje. Jos gali būti taikomos įvairiose srityse, tokiose kaip:

1. Ekonomika: Naudojamos modeliuojant pasiūlą ir paklausą.
2. Inžinerija: Aprašant įvairių dydžių santykius, pavyzdžiui, įtampą ir srovę.
3. Fizika: Taikomos aprašyti judėjimo dėsnius, tokius kaip greitis ir pagreitis.

Kaip Brėžti Tiesinę Funkciją?

Braižant tiesinę funkciją, svarbu žinoti, kaip nustatyti jos koeficientus. Štai keli žingsniai, kaip tai padaryti:

1. Nustatykite k (kampinį koeficientą) ir b (pradžios tašką).
2. Braižykite tašką (0, b) ant grafiko.
3. Panaudokite k, kad nustatytumėte kitus taškus, pavyzdžiui, (1, k + b).
4. Suformuokite tiesę, jungdami visus taškus.

Pavyzdys

Tarkime, turime tiesinę funkciją f(x) = 2x + 3. Šiuo atveju:

• kampinis koeficientas (k) yra 2, tai reiškia, kad tiesinė funkcija kyla 2 vienetais už kiekvieną 1 vienetą, judant į dešinę.
• pradžios taškas (0, 3) rodo, kad kai x = 0, f(x) = 3.

Apibendrinimas

Tiesinės funkcijos yra esminis matematikos konceptas, padedantis suprasti ir modeliuoti tiesinę priklausomybę. Jos taikomos įvairiose mokslo ir inžinerijos srityse, todėl svarbu gerai išmanyti šio tipo funkcijas. Daugiau apie tai galima sužinoti čia.