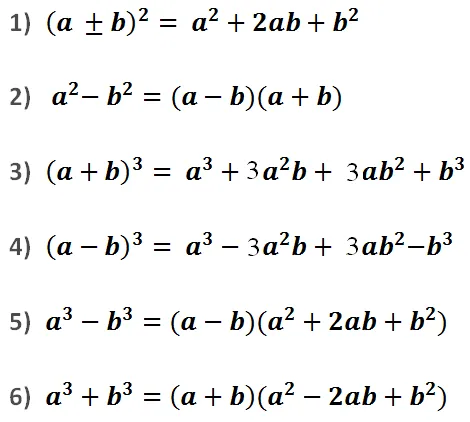
Greitosios Daugybos Formulės: Efektyvūs Matematikos Įrankiai

Matematika gali atrodyti sudėtinga, tačiau tam tikrų formulių ir taisyklių išmanymas gali žymiai palengvinti skaičiavimus. Šiame straipsnyje aptarsime greitosios daugybos formules, kurios leis jums greičiau ir efektyviau atlikti matematikos užduotis.

Greitosios Daugybos Taisyklės

Greitosios daugybos formulės yra puikus įrankis, leidžiantis greitai atlikti tam tikrus matematikos veiksmus. Jos yra naudingos dirbant su daugianariais, o taip pat ir kitose matematikos srityse.

Pirmoji Taisyklė: Dviejų Narių Sumos Kėlimas Kvadratu

Ši formulė leidžia išreikšti kvadratą, gautą iš dviejų reikšmių sumos:

(a + b)² = a² + 2ab + b²

Pavyzdžiui, apskaičiuojant (3 + 4)², galime greitai gauti rezultatą:

(3 + 4)² = 3² + 2 * 3 * 4 + 4² = 49

Antroji Taisyklė: Dviejų Narių Skirtumo Kėlimas Kvadratu

Formulė, naudojama dviejų narių skirtumui kvadratuoti, yra:

(a – b)² = a² – 2ab + b²

Pavyzdžiui, apskaičiuojant (5 – 2)²:

(5 – 2)² = 5² – 2 * 5 * 2 + 2² = 9

Trečioji Taisyklė: Dviejų Narių Sumos ir Skirtumo Sandauga

Ši formulė leidžia išreikšti pirmojo nario kvadratą ir antrojo nario kvadratą:

(a + b) * (a – b) = a² – b²

Pavyzdys:

(9² – 4²) = (9 + 4)(9 – 4) = 13 * 5 = 65

Priedai: Sumos ir Skirtumo Kubas

Kubų formules taip pat galima pritaikyti:

• Sumos kubas: (a + b)³ = a³ + 3a²b + 3ab² + b³
• Skirtumo kubas: (a – b)³ = a³ – 3a²b + 3ab² – b³

Skaidymas Dauginamaisiais

Skaidymo metodas leidžia išreikšti daugianarių sandaugas, pavyzdžiui: ab + ac = a(b + c).

Bendro Daliklio Iškėlimas Prieš Skliaustus

Bendro daliklio iškėlimas leidžia išreikšti bendrą daliklį kaip faktorinį daugiklį:

ab + ac = a(b + c).

Grupavimo Metodas

Grupavimo metodas yra matematinis metodas, leidžiantis išreikšti daugianarius kaip sandaugą daugiklių grupėmis. Pavyzdžiui, nagrinėkime išraišką ab + cd + ad + cb. Galime grupuoti ją į dvi grupes:

• ab + cd = a(b + d)
• ad + cb = c(a + b)

Panaudojus šias grupes, galime išreikšti pradinį daugiklį:

ab + cd + ad + cb = a(b + d) + c(a + b).

Apibendrinimas

Greitosios daugybos formules ir metodai yra esminiai įrankiai, padedantys efektyviai atlikti skaičiavimus ir taupyti laiką. Supratę ir išmokę taikyti šias formules, būsite gerokai pasiruošę matematikos užduotims. Nepriklausomai nuo to, ar sprendžiate sudėtingas problemas, ar ieškote paprastų sprendimų, šios taisyklės gali būti naudingos.

Daugiau informacijos apie matematiką ir skaičiavimus rasite šiame straipsnyje.