Atvirkštinė Funkcija: Apibrėžimas ir Pavyzdžiai

Atvirkštinė funkcija yra matematinis konceptas, kuris apibūdina aibės Y elementų atvaizdavimą į aibę X. Tai yra, kiekvienam elementui y ∈ Y priskiriamas atitinkamas elementas x ∈ X, remiantis funkcijos f, kuri atitinka x → y, apibrėžimu. Pavyzdžiui, funkcija, kuri atvaizduoja x į y = x^2, kai ji apibrėžta intervale X = [–2, –1], atvaizduoja į intervalą Y = [1, 4]. Tokiu atveju, atvirkštinė funkcija egzistuoja tik tada, kai skirtingiems aibės X elementams atitinka skirtingos funkcijos reikšmės.

Atvirkštinės Funkcijos Savybės

Atvirkštinė funkcija, pažymima kaip f^–1(y), yra apibrėžta tik tada, kai funkcija f yra abipusiškai vienareikšmė. Tai reiškia, kad kiekvienam y ∈ Y turi būti priskiriamas unikalus x ∈ X. Jei f yra funkcija, tai grafikuose f ir f^–1 sutampa, kai X ir Y yra realiųjų skaičių aibės.

Pavyzdžiai

• Funkcija f(x) = x² (x ∈ [–2, –1]) turi atvirkštinę funkciją f^–1(y) = √y.
• Funkcija f(x) = e^x (x ∈ R) turi atvirkštinę funkciją f^–1(y) = ln(y).
• Funkcija f(x) = sen(x) (x ∈ [–π/2, π/2]) turi atvirkštinę funkciją f^–1(y) = arcsen(y).

Trigonometrinės Atvirkštinės Funkcijos

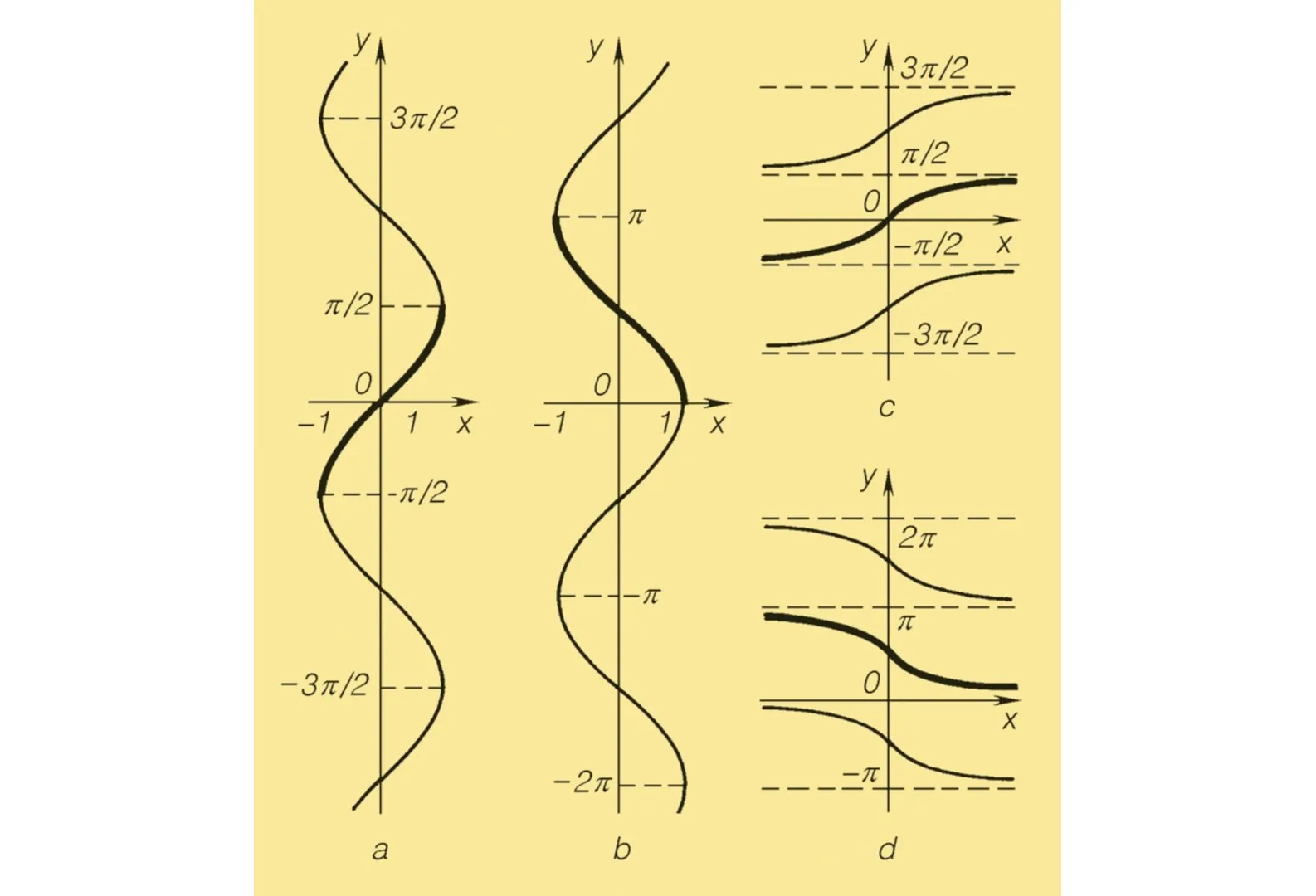
Atvirkštinės trigonometrinės funkcijos, tokios kaip arcsin, arccos, arctan, ir arccot, yra svarbios matematikos srityje. Jos dažnai naudojamos sprendžiant trikampius ir analizuojant funkcijas. Pavyzdžiui:

• y = arcsin(x): Tai atvirkštinė funkcija sinusui, kurios apibrėžimo sritis yra –1 ≤ x ≤ 1, o reikšmės sritis – [–π/2, π/2].
• y = arccos(x): Atvirkštinė funkcija kosinuso, su ta pačia apibrėžimo sritimi, bet reikšmių sritis yra [0, π].
• y = arctan(x): Apibrėžta visiems realiesiems skaičiams, su reikšmės sritimi (–π/2, π/2).

Atvirkštinės Trigonometrinės Funkcijos ir jų Savybės

Atvirkštinės trigonometrinės funkcijos turi keletą svarbių savybių, kurios padeda jas analizuoti:

• Jos yra abipusiškai vienareikšmės, todėl kiekvienai iš jų galima rasti atvirkštinę.
• Jos gali būti išskleidžiamos į Tayloro eilutes, leidžiančias apskaičiuoti jų reikšmes.
• Grafikai rodo, kaip šios funkcijos keičiasi, ir gali būti naudojami sprendžiant trigonometrines lygtis.

Praktinis Panaudojimas

Atvirkštinės funkcijos plačiai naudojamos įvairiose matematikos srityse, įskaitant:

• Matematinis modeliavimas.
• Statistika, ypač regresijų analizėje.
• Inžinerija, sprendžiant techninius uždavinius.

Atvirkštinių Funkcijų Grafikai

Grafikai leidžia vizualizuoti atvirkštines funkcijas ir suprasti jų elgseną. Pavyzdžiui, grafikai f(x) = x² ir f^–1(y) = √y yra simetriški, o tai iliustruoja atvirkštinio proceso principą.

Apibendrinimas

Atvirkštinės funkcijos yra esminis matematinių koncepcijų aspektas, padedantis suprasti, kaip skirtingi elementai sąveikauja tarpusavyje. Sužinojus apie jų savybes ir pavyzdžius, galima geriau įvaldyti matematikos principus ir juos taikyti praktikoje. Jei norite sužinoti daugiau, rekomenduojame perskaityti Integralai: Matematika ir jų taikymas.