Trikampio Ploto Apskaičiavimas: Formulės ir Pavyzdžiai

Trikampis – tai geometrinė figūra, turinti tris viršūnes ir kraštines, jungiančias šias viršūnes. Trikampio plotas yra erdvė, kurią ši figūra užima, ir jis gali būti apskaičiuojamas keliais būdais, priklausomai nuo turimų duomenų. Šiame straipsnyje aptarsime, kaip apskaičiuoti trikampio plotą, naudojant trikampio ploto formulę, lygiašonio trikampio savybes ir pateiksime keletą pavyzdžių.

Kaip Apskaičiuoti Trikampio Plotą?

Trikampio ploto skaičiavimas dažnai remiasi žiniomis apie trikampio pagrindą ir aukštinę. Pagrindinė trikampio ploto formulė yra:

S = (a * h) / 2

• S – trikampio plotas (kvadratiniai matavimo vienetai, pavyzdžiui, cm², m² ir pan.),
• a – trikampio pagrindo ilgis (cm, m ir pan.),
• h – trikampio aukštinės ilgis (cm, m ir pan.).

Trikampio aukštinė yra statmuo, kuris eina iš trikampio viršūnės iki pagrindo.

Pavyzdys

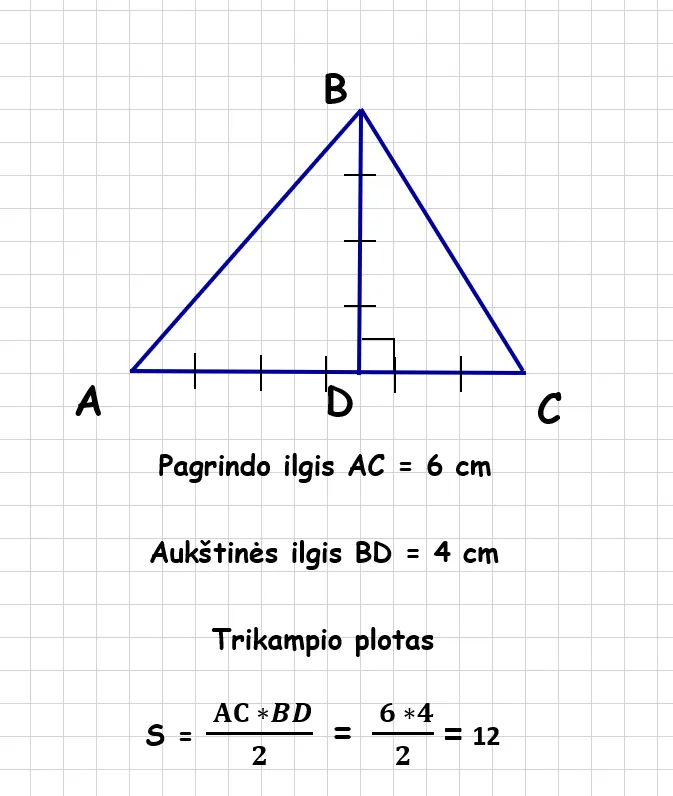
Pavyzdžiui, jei turime trikampį, kurio pagrindo ilgis yra 6 cm, o aukštinės ilgis – 4 cm, trikampio plotas bus:

S = (6 cm * 4 cm) / 2 = 12 cm²

Statusis Trikampis

Statusis trikampis yra toks trikampis, kurio vienas kampas yra 90 laipsnių. Jis turi specialią ploto apskaičiavimo formulę:

S = (a * b) / 2

Čia:

• a ir b – statiniai, kurie sudaro stačiuosius kampus.

Pavyzdžiui, jei turime stačiąjį trikampį su statiniais, kurių ilgiai yra 3 cm ir 4 cm, plotas bus:

S = (3 cm * 4 cm) / 2 = 6 cm²

Lygiašonis Trikampis

Lygiašonis trikampis yra trikampis, kurio dvi kraštinės yra lygios. Šio trikampio plotą taip pat galima apskaičiuoti naudojant aukščiau minėtą formulę, tačiau galima taikyti ir kitą metodą, kai žinomas aukštinės ilgis.

Pavyzdžiui, jeigu turime lygiašonį trikampį, kurio pagrindo ilgis yra 6 cm, o aukštinės ilgis – 8 cm, trikampio plotas bus:

S = (6 cm * 8 cm) / 2 = 24 cm²

Pitagoro Teorema

Pitagoro teorema taip pat gali būti naudinga, kai reikia apskaičiuoti lygiašonio trikampio aukštinę, nubrėžtą į pagrindą. Jei žinome šoninių kraštinių ilgius ir pagrindo ilgį, galime naudoti šią teoremą:

a² = b² + h²

Kur:

• a – lygiašonio trikampio šoninės kraštinės ilgis,
• b – pusė pagrindo ilgis,
• h – trikampio aukštinės ilgis.

Pagal šią formulę galime apskaičiuoti h:

h = √(a² – b²)

Pavyzdys su Pitagoro Teorema

Tarkime, turime lygiašonį trikampį, kuriame kraštinių ilgiai yra 5 cm, o pagrindo ilgis 6 cm. Pirmiausia apskaičiuokime pusę pagrindo ilgį:

b = 6 cm / 2 = 3 cm

Dabar galime apskaičiuoti aukštinės ilgį:

h = √(5² – 3²) = √(25 – 9) = √16 = 4 cm

Dabar galime rasti trikampio plotą:

S = (6 cm * 4 cm) / 2 = 12 cm²

Trikampio Ploto Skaičiavimo Įrankiai

Yra įvairių internetinių skaičiuotuvų, kurie gali padėti apskaičiuoti trikampio plotą, naudojant skirtingus metodus, pavyzdžiui, žinant kraštinių ilgius, kampus ar kitus parametrus. Galite pasinaudoti šiais įrankiais, kad gautumėte greitus ir tikslius rezultatus.

Išvados

Pabaigai, trikampio ploto apskaičiavimas yra svarbus matematikos aspektas, kurį galima atlikti įvairiais būdais, priklausomai nuo turimų duomenų. Nepamirškite, kad tinkama formulė gali padėti greitai ir tiksliai apskaičiuoti plotą, o žinios apie trikampių tipus ir jų savybes padės geriau suprasti geometriją.

Norėdami sužinoti daugiau apie matematikos pagrindus, apsilankykite mūsų svetainėje ir atraskite naudingus patarimus ir straipsnius.