Diskriminantas ir Jo Nauda Kvadratinių Lygių Sprendime

Diskriminantas yra svarbus matematikos elementas, ypač algebroje, nes jis leidžia nustatyti, kiek sprendinių turi kvadratinė lygtis. Kvadratinė lygtis turi formą ax² + bx + c = 0, kur a, b ir c yra koeficientai.

Diskriminanto Formulė

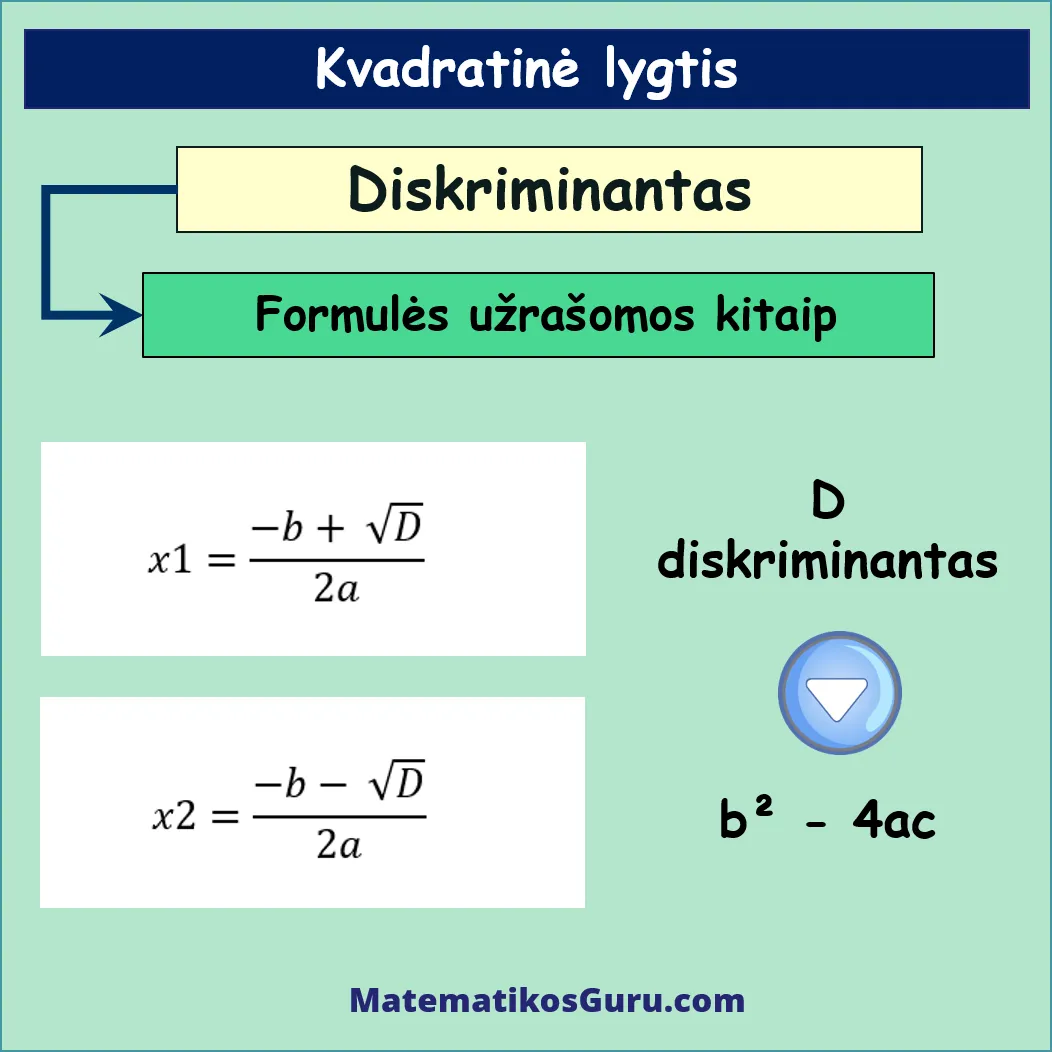
Diskriminantas žymimas raide D ir apskaičiuojamas pagal formulę:

D = b² – 4ac

Ši formulė leidžia greitai nustatyti sprendinių skaičių:

• D > 0: Lygtis turi du skirtingus realius sprendinius.
• D = 0: Lygtis turi vieną realų sprendinį.
• D < 0: Lygtis neturi realių sprendinių (sprendiniai yra kompleksiniai skaičiai).

Pavyzdys

Paimkime kvadratinę lygtį 2x² – 3x + 1 = 0. Pirmiausia, nurodome koeficientus:

• a = 2
• b = -3
• c = 1

Dabar apskaičiuokime diskriminantą:

D = (-3)² – 4 * 2 * 1 = 9 – 8 = 1

Kadangi D = 1 (didesnis už 0), žinome, kad lygtis turi du skirtingus sprendinius. Ištraukime šaknį iš diskriminanto:

√D = √1 = 1

Dabar galime apskaičiuoti sprendinius pagal kvadratinės lygties formulę:

• x₁ = (−b + √D) / (2a) = (3 + 1) / (4) = 1
• x₂ = (−b – √D) / (2a) = (3 – 1) / (4) = 1/2

Patikrinkime, ar šie sprendiniai teisingi:

• Įstatydami x₁ = 1: 2(1)² – 3(1) + 1 = 2 – 3 + 1 = 0 ➡️ Teisinga.
• Įstatydami x₂ = 1/2: 2(1/2)² – 3(1/2) + 1 = 0 ➡️ Teisinga.

Diskriminanto Nauda

Diskriminantas ne tik padeda nustatyti sprendinių skaičių, bet ir leidžia suprasti kvadratinių lygių savybes. Pavyzdžiui, žinodami, kad D < 0, galime pasakyti, jog lygtis neturi realių sprendinių, kas gali būti naudinga analizuojant problemas įvairiose srityse, tokiose kaip fizika ar inžinerija.

Apibendrinimas

Diskriminantas yra esminis įrankis sprendžiant kvadratines lygtis, leidžiantis greitai įvertinti sprendinių skaičių ir pobūdį. Jo formulė D = b² – 4ac yra universali ir plačiai naudojama matematikos srityje. Norint išmokti daugiau apie kvadratinių lygių sprendimą, galite apsilankyti šioje nuorodoje.